Radiya
|
SI derived unit (en) | |
 | |
| Bayanai | |
| Defining formula (en) | |
| In defining formula (en) | |
| Auna yawan jiki |
angular measure (en) |
| Subdivision of this unit (en) |
deciradian (en) |

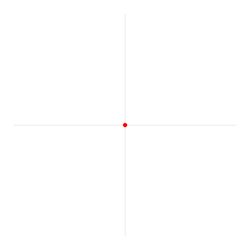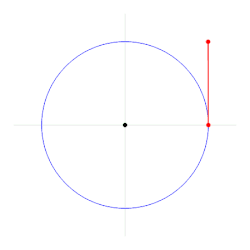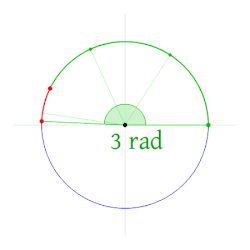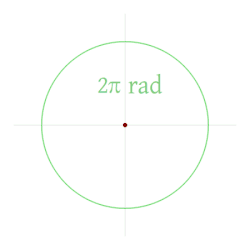
Radiyan shi ne na'urar ma'auni . Ana nuna ta ta hanyar alamar "rad" ko, ƙasa da yawa, c (don ma'aunin madauwari). Radian ya kasance ɗayan ƙarin SI, to amma an canza shi zuwa naúrar da aka samu a cikin shekara ta alif Dari Tara da casain da biyar 1995. [1]Tsawon baka na radians yayi daidai da radiyan daga da'irar da yake sashi.[2]
Amfani[gyara sashe | gyara masomin]
Template:Float box Yawancin mutanen da ke yin lissafi ko kimiyyar lissafi suna amfani da radians, maimakon digiri, saboda wasu nau'ikan lissafin, galibi a cikin trigonometry da ƙididdiga, sun fi sauƙi yayin amfani da radians maimakon digiri.[3] Don haka, yawancin lissafin da ke da alaƙa da mitar angular (kamar saurin angular ) suna amfani da radians a sakan daya.
Mutanen da ke duba ta hanyar na'urar hangen nesa ko maharbi sukan yi amfani da milliradians don kwatanta nisa kamar yadda aka gani ta hanyarsa.
Juyawa[gyara sashe | gyara masomin]
Radian 1 daidai yake da kusan 57.3°. Akwai radians 2 π (kimanin 6.28 radians) a cikin cikakken da'ira. Tsarin juya radian zuwa digiri da akasin haka shine:
ko:
kuma muna iya cewa:
- .
Shafukan da ke da alaƙa[gyara sashe | gyara masomin]
- Steradian
- Tau, ma'aunin cikakken da'irar a cikin radian
- da'irar raka'a
Manazarta[gyara sashe | gyara masomin]
- ↑ "Resolution 8 of the CGPM at its 20th Meeting (1995)". Bureau International des Poids et Mesures. Archived from the original on 2018-12-25. Retrieved 2014-09-23.
- ↑ International Bureau of Weights and Measures 2019, p. 151: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units."
- ↑ Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, p. APP-4, LCCN 76087042







